▤ 목차
Introduction to Probability and Probability Distributions
Probability Distributions
Probability Distributions (Continuous)
In the discrete distributions, the events always form a list of elements.
In the continuous distributions, the events are an interval.

What is the probability that you will wait exactly one minute for the call?
0
Correct. Too many values for the amount of time a call can take



Probability Density Function
With continuous distributions, we cannot make a count of the probabilities.
Instead, we put them in intervals and that’s called a probability density function.
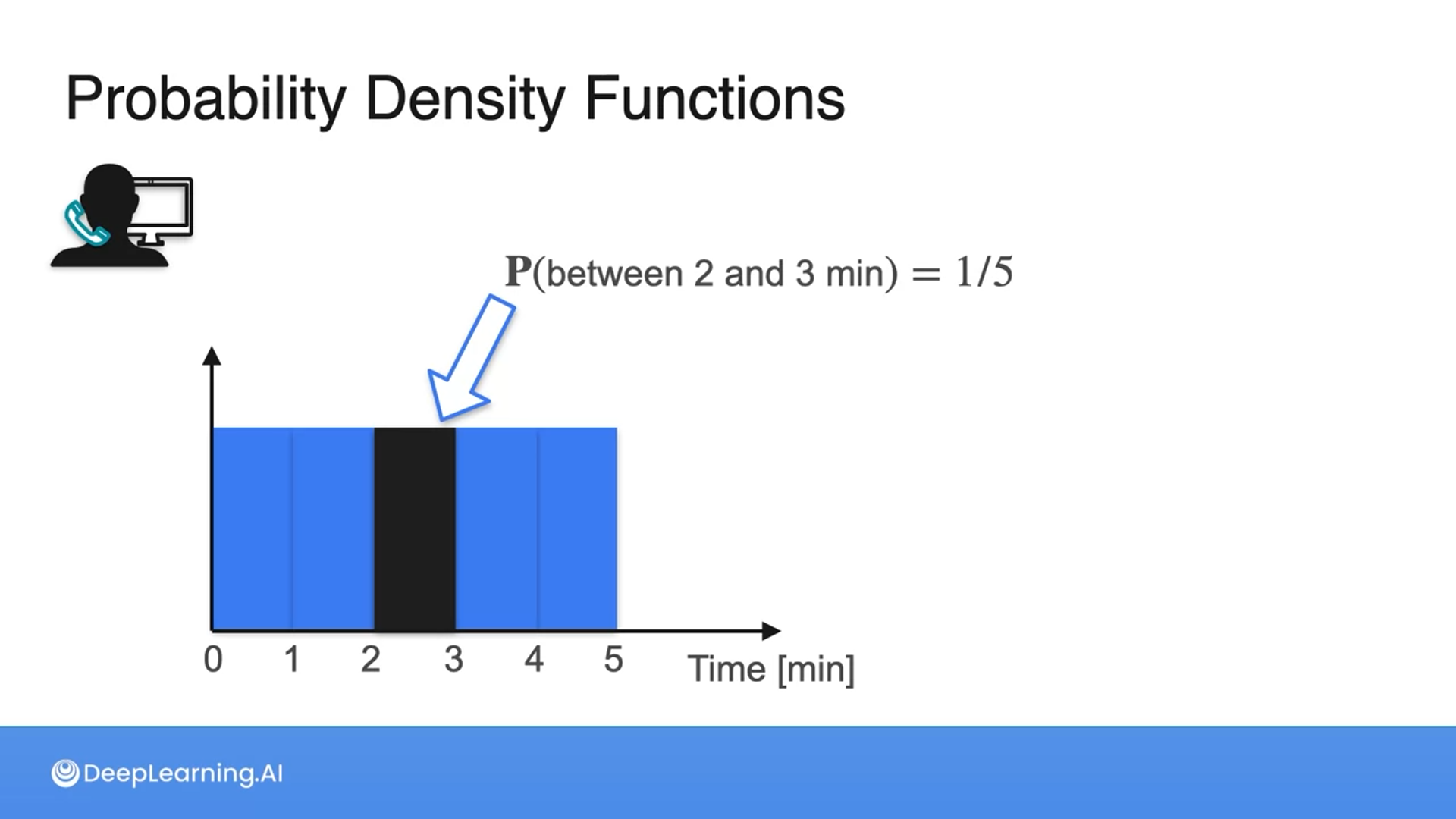
What is the probability that the call is between 2 and 3 minutes long if all calls are in 5 equal intervals, i.e., what is the value of P(between 2 and 3)?
20%
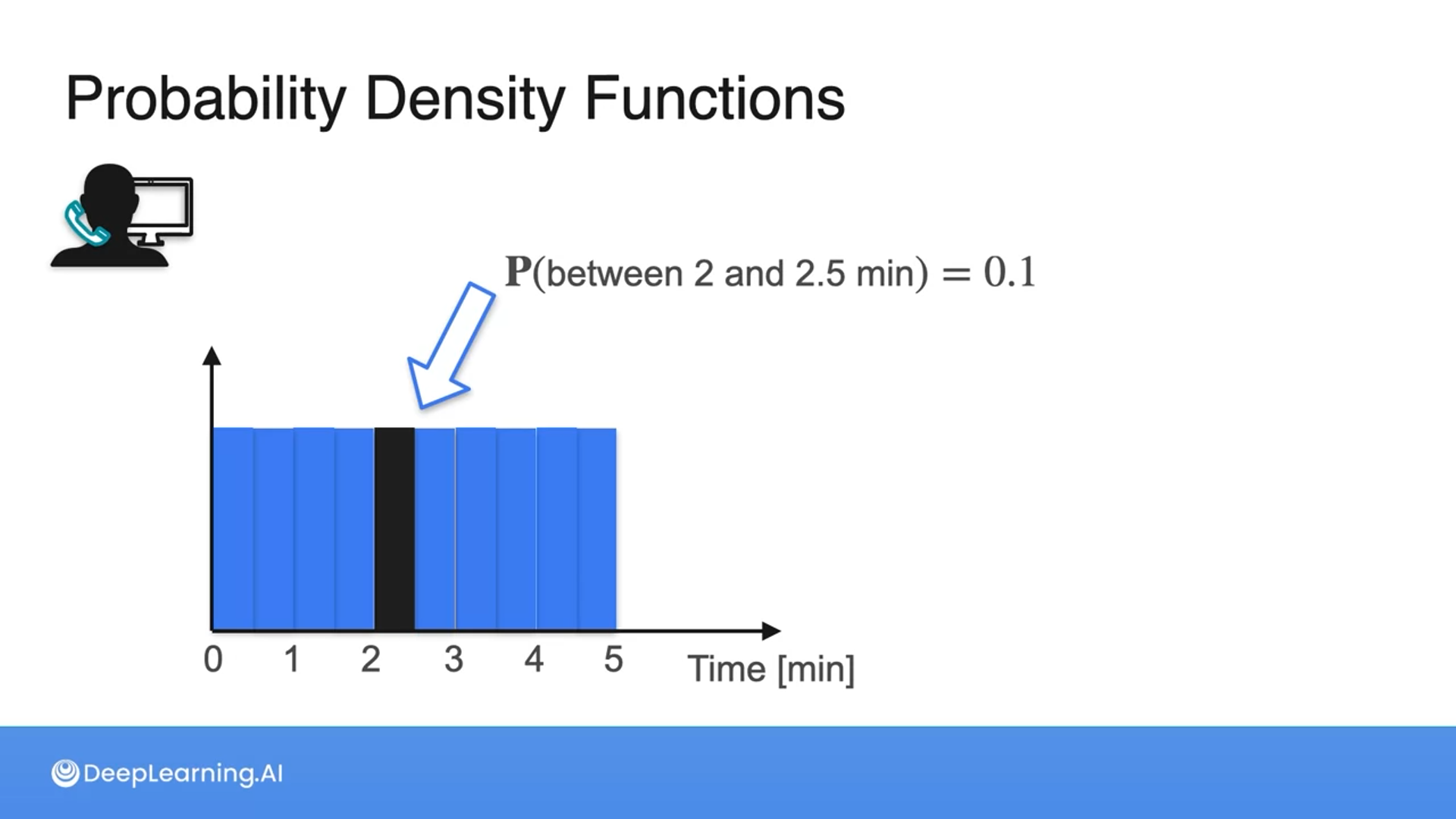
What is the probability that the call is between 2 and 2.5 minutes long if all calls are in 10 equal intervals, i.e., what is the value of P(between 2 and 2.5)?
10%


We don’t look at the probability of a certain value since the area of a single value is 0, instead, we look at intervals and the area of an interval is a probability.

The probability density function (PDF) with continuous distributions is equivalent to the probability mass function (PMF) with discrete distributions.

Cumulative Distribution Function
The cumulative distribution function shows the actual probability between certain numbers (before certain reference points) and makes it more convenient to calculate the area.
Cumulative distribution function also exists for discrete distributions.

With discrete distributions, we get jumps in density when we plot CDFs and planks at 1 since we can’t accumulate any more.
It always starts at 0 and ends at 1.
What is the maximum possible value that the cumulative distribution function can reach?
1
Individual CDFs can vary and potentially reach any value between 0 and 1. However, CDFs, in general, will have a maximum value of 1 as it represents the total probability of all possible outcomes.


With continuous distributions, we don’t get jumps in density because each point doesn’t have probability mass on its own and once we don’t have points with mass, we don’t see any jumps, hence, the CDF curve is smooth instead of a stair-looking shape.



Properties of CDF:
- Y (vertical) values have to be between 0 and
- The left “endpoint” of the Y (vertical) value is 0
- The right “endpoint” of the Y (vertical) value is 1
- Never decreases
All the information provided is based on the Probability & Statistics for Machine Learning & Data Science | Coursera from DeepLearning.AI




 }
}