Linear Algebra for Machine Learning and Data Science (1)

Systems of linear equations

Matrices are commonly used in machine learning and data science to represent data and its transformations. This week, you will learn how matrices naturally arise from systems of equations and how certain matrix properties can be thought of in terms of operations on systems of equations.

Learning Objectives

• Form and graphically interpret 2x2 and 3x3 systems of linear equations
• Determine the number of solutions to a 2x2 and 3x3 system of linear equations
• Distinguish between singular and non-singular systems of equations
• Determine the singularity of the 2x2 and 3x3 system of equations by calculating the determinant

Systems of Equations

Linear Algebra Applied

Linear: It can be modeled by a line

Linear regression: Given data can be modeled by a line

Example of linear regression to predict the electrical power output using wind speed as an input

Here we want to find the ideal weights and bias of the given data (multiple features and multiple examples)

Since finding weights and bias uses the concept of linear algebra (y = wx + b) on multiple examples, it’s called a system of linear equations

With the model knowing its weights (w) and biases (b), it can find the target (y) when features (x) are given

Example of linear equations where the weights and variables ($x$) are features

System of sentences

The system of sentences behaves like the system of equations

The goal of a system is to convey as much information as possible with these simple sentences

Complete system: When the system contains as many pieces of information as sentences

Redundant system: When the system contains information that repeats itself in sentences

Contradictory system: When the system contains sentences that contract each other

01

Examples of complete, redundant, and contradictory systems

More information = more useful

Try and solve this quiz

Since the color of the dog is black, and orange for cat, the color of the bird is red

 

The system carries as many pieces of information as sentences meaning that it is a complete system, which is called non-singular.

System of equations

Simply put we can turn the system of sentences into equations

Example of sentences to equations

Try to solve this quiz

Apple = $8, Banana = $2

You can replace these values with the equations to check that they're indeed correct.

Try to solve this quiz

Here we can turn sentences into equations like the following:

a + b + c = 10

a + 2b + c = 15

a + b + 2c = 12

 

Thus, Apple = $3, Banana = $5 and Cherry = $2

Linear vs non-linear equations

System of equations as lines and planes

If we were to have two lines anywhere on a 2-D plane we can either have a unique solution, infinitely many solutions, or no solutions. Please take a look at the below slide to gain an understanding of the visual.

Three distinct solutions

Try to solve this quiz

Plot a) is the answer

The system of equations has a unique solution at point (2, 1), which is the point where the equation lines intersect.

 

The system is complete and has a unique solution at point (2, 1). Therefore, the system of equations is non-singular.

If we were to have a linear equation with 3 variables and have a plot on a 3-D plane, we can see singular and non-singular planes as the following:

012

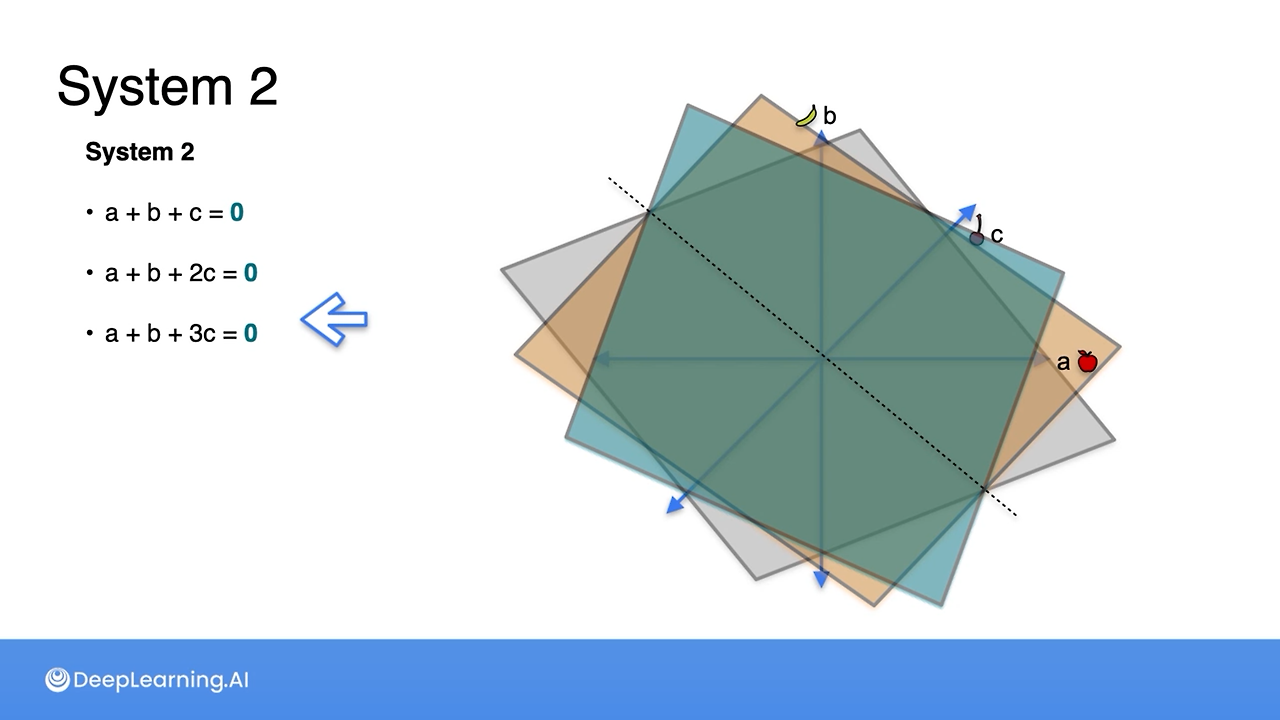
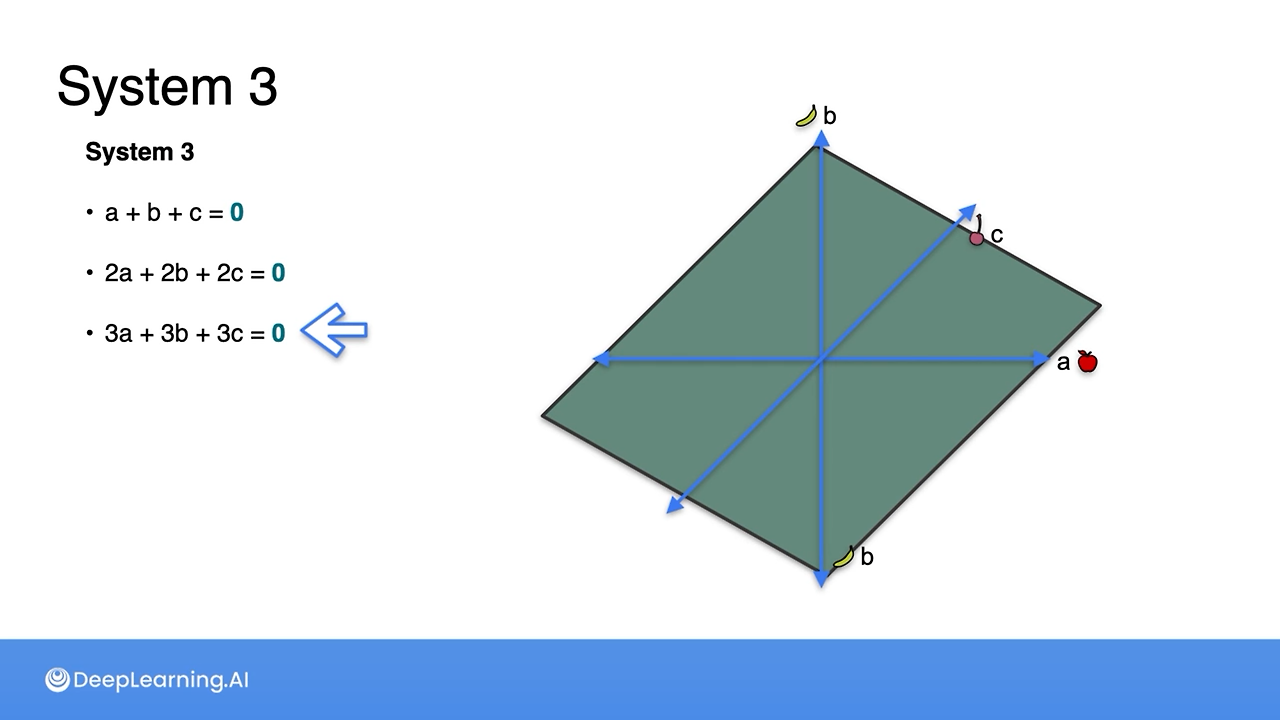
System 1:  Non-singular (has a unique solution)

System 2: Singular (has infinitely many solutions on a dotted line)

System 3: Singular (every set of points on a plane are solutions)

 

All the information here is based on the Linear Algebra for Machine Learning and Data Science | Coursera from DeepLearning.AI