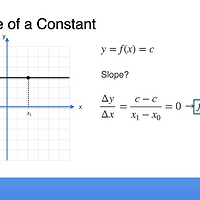
Derivatives and Optimization
Quiz
Q1
Consider the following lines.
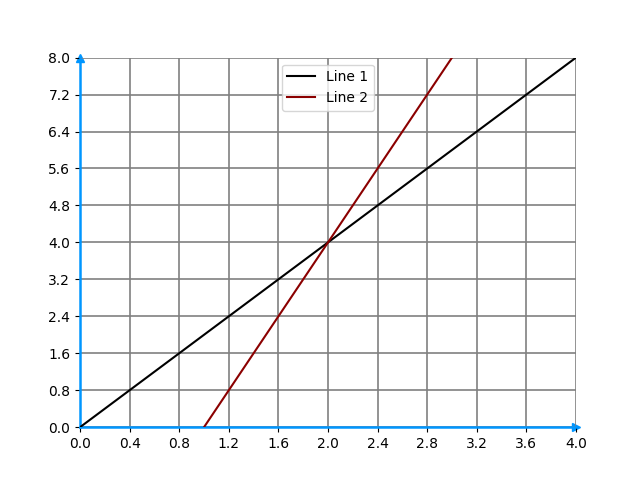
What can be said about the slopes at their intersection?
- Slope(Line 1) > Slope(Line 2).
- Slope(Line 1) < Slope(Line 2).
- Slope(Line 1) = Slope(Line 2).
- It is impossible to infer anything from the given information.
Answer
2
Correct! Line 2 is steeper than Line 1, therefore its slope is higher.
Q2
Given the following graph, what is the slope of the line? You can pick any two points to calculate the slope.
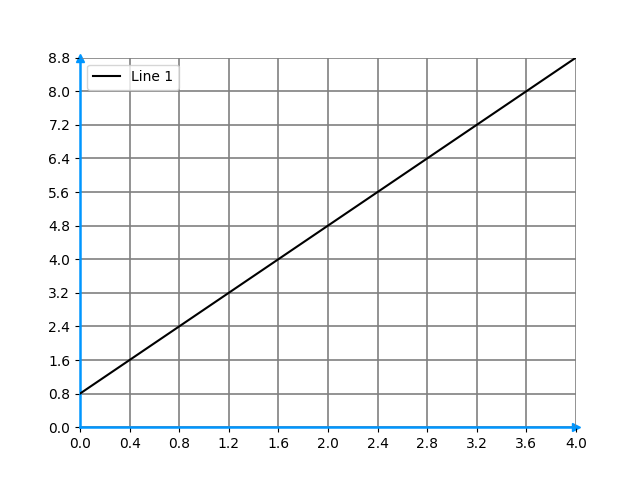
Answer
2
Correct! For a line, the slope is ${\Delta f \over \Delta x}$
Q3
Consider the graphs below
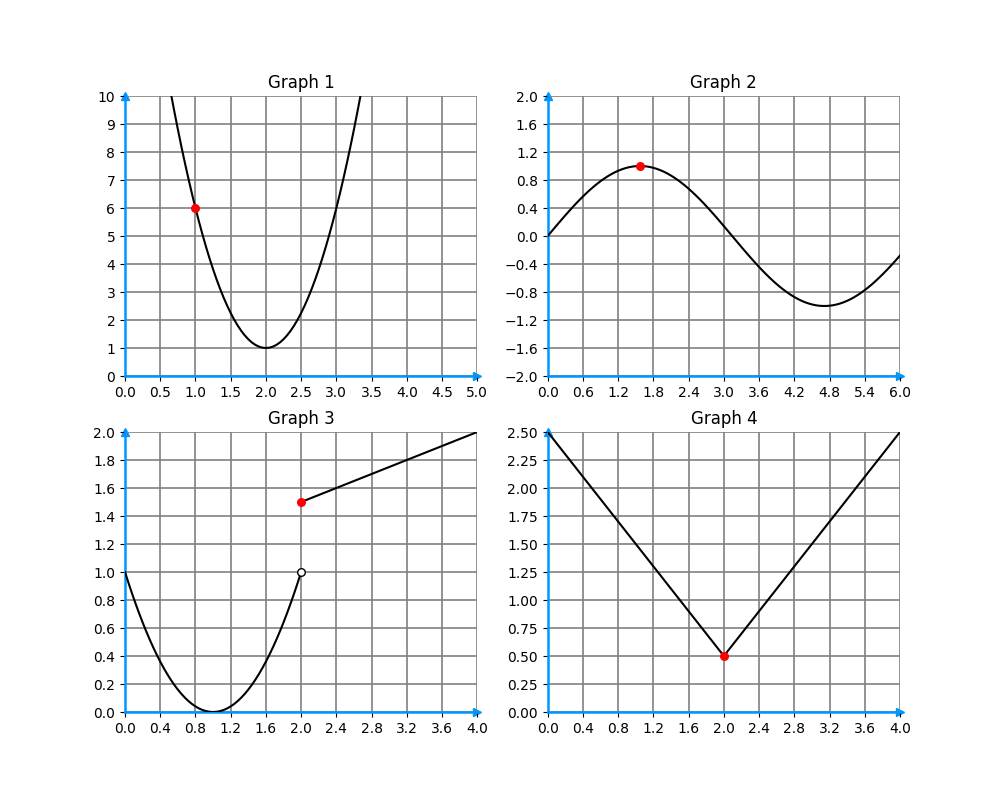
What can be said about the curve’s slopes at the red point, which we will call P1, P2, P3, and P4, corresponding to the red points in graphs 1, 2, 3, and 4, respectively?
- Slope(P1) > 0, Slope(P2) < 0, Slope(P3) does not exist, Slope(P4) = 0.
- Slope(P1) < 0, Slope(P2) = 0, Slope(P3) > 0, Slope(P4) does not exist.
- Slope(P1) < 0, Slope(P2) = 0, Slope(P3) does not exist, Slope(P4) does not exist.
- Slope(P1) < 0, Slope(P2) = 0, Slope(P3) does not exist, Slope(P4) > 0.
Answer
3
Q4
Let $y_1 = ax + b$ and $y_2 = cx+d$, where $a, b, c, d \in \R$. Check all true sentences
- The slope of $y_1$ is $a$
- The slope of $y_1$ is $-{b\over a}$
- If $a > c$ then the slope of $y_1$ is greater than the slope of $y_2$
- The slope of $y_1$ does not depend on $b$
Answer
1
Correct! For a line, its rate of change depends only on $a$, since it is the only factor that varies in the expression.
3
Correct! Remember that the slope of a line is the value that comes with the $x$
4
Correct! In this case, $b$ is a constant term and, therefore, does not impact the rate of change.
Q5
Which of the following sentences are true (check all that apply)?
- If the slope of a function is constant, then the function is constant.
- If the slope of a function is always positive, then the function is always positive.
- Let $f,g$ be real functions. If $f'(x)>g'(x)$ then $f(x)>g(x)$.
- Let $f$ be a real function. If $f'(x)>0$ for every $x$ in $\R$, then $f$ is increasing.
Hint
Keep in mind that the slope tells us about the rate of change of a function and not about its values.
Answer
4
Correct! If the rate of change of a function is always positive, it means that it is always increasing.
All the information provided is based on the Calculus for Machine Learning and Data Science | Coursera from DeepLearning.AI
'Coursera > Mathematics for ML and Data Science' 카테고리의 다른 글
| Calculus for Machine Learning and Data Science (6) (0) | 2024.08.27 |
|---|---|
| Calculus for Machine Learning and Data Science (5) (0) | 2024.08.26 |
| Calculus for Machine Learning and Data Science (3) (0) | 2024.08.24 |
| Calculus for Machine Learning and Data Science (2) (0) | 2024.08.23 |
| Calculus for Machine Learning and Data Science (1) (0) | 2024.08.22 |