▤ 목차
Confidence Intervals and Hypothesis testing
Hypothesis Testing
Defining Hypotheses



The null hypothesis is when nothing is happening.
The alternative hypothesis is when something is happening and something we want to prove using the data.
Rejecting the alternative hypothesis means we don’t have enough evidence, but it doesn’t mean we accept the null hypothesis.
We are simply rejecting the hypothesis and not accepting the other.
Refer to this for more information.
Type I and Type II errors


Type 1 error happens when we reject the null hypothesis, although it is true.
The example labeled the email as spam, although it was not.
Type 2 error happens when we don’t reject the null hypothesis, although it is false.
The example labeled the email as ham, although it was not.





A significance level is the maximum probability of committing a type 1 error, which is the same as the maximum probability of rejecting the null hypothesis ($H_0$) when it is true.
Right-Tailed, Left-Tailed, and Two-Tailed Tests


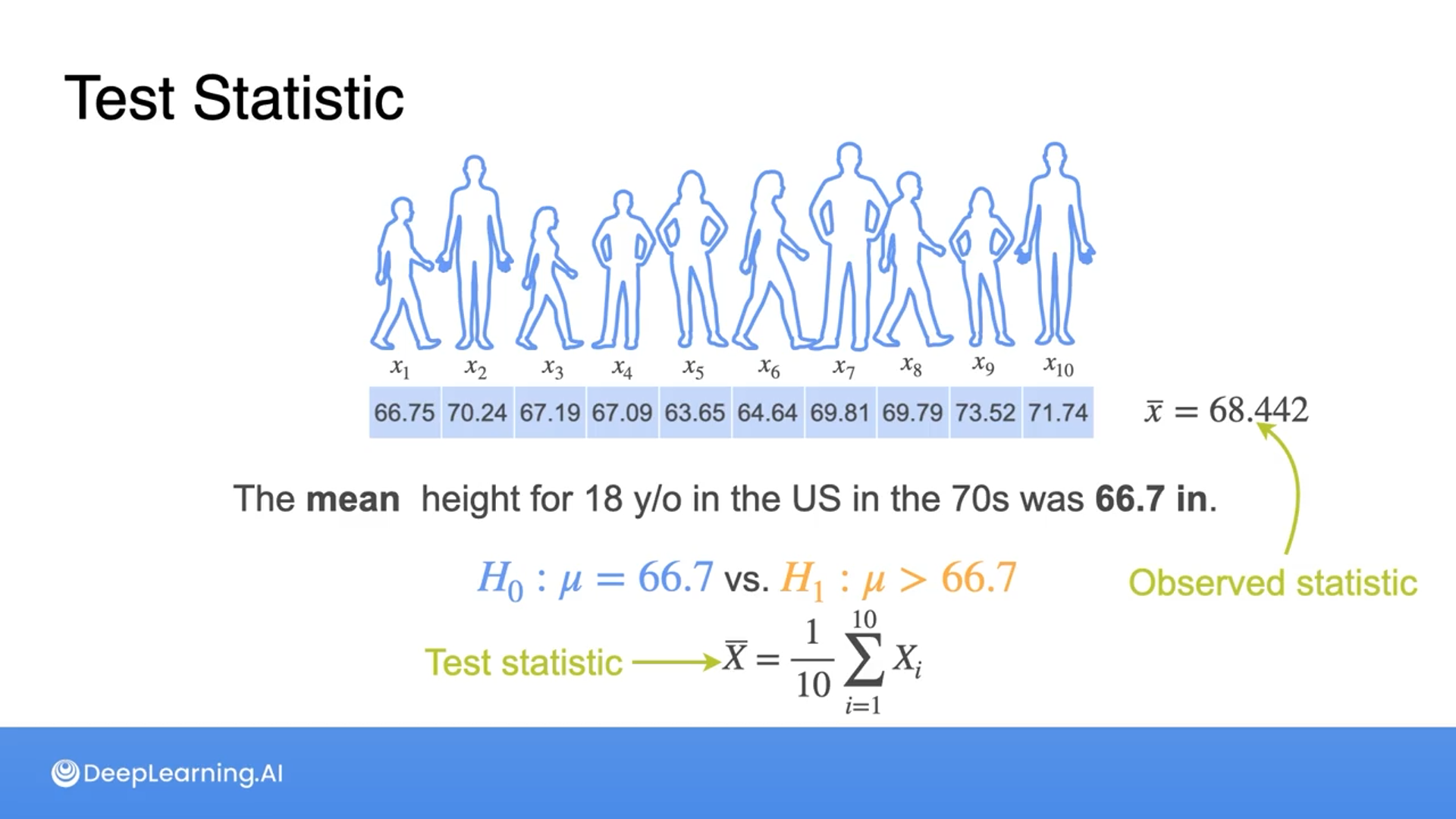

We need data to be reliable.
The hypothesis is always formulated from the population, not from the sample.
In the example, we use the population mean.
However, the decision will be based on the observations we have.
In the example, we use the sample mean which is called the observed statistic.
If we use the sample mean to make a decision, then the sample mean is called the test statistic, a random variable that doesn’t depend on the particular observations yet.
In general, a test statistic will be a function of random samples that gives the info about the population parameter under study.
It’s not unique and can be any function like the formula for the variance, which is the value minus the mean.

We change the alternative hypothesis depending on the goal.



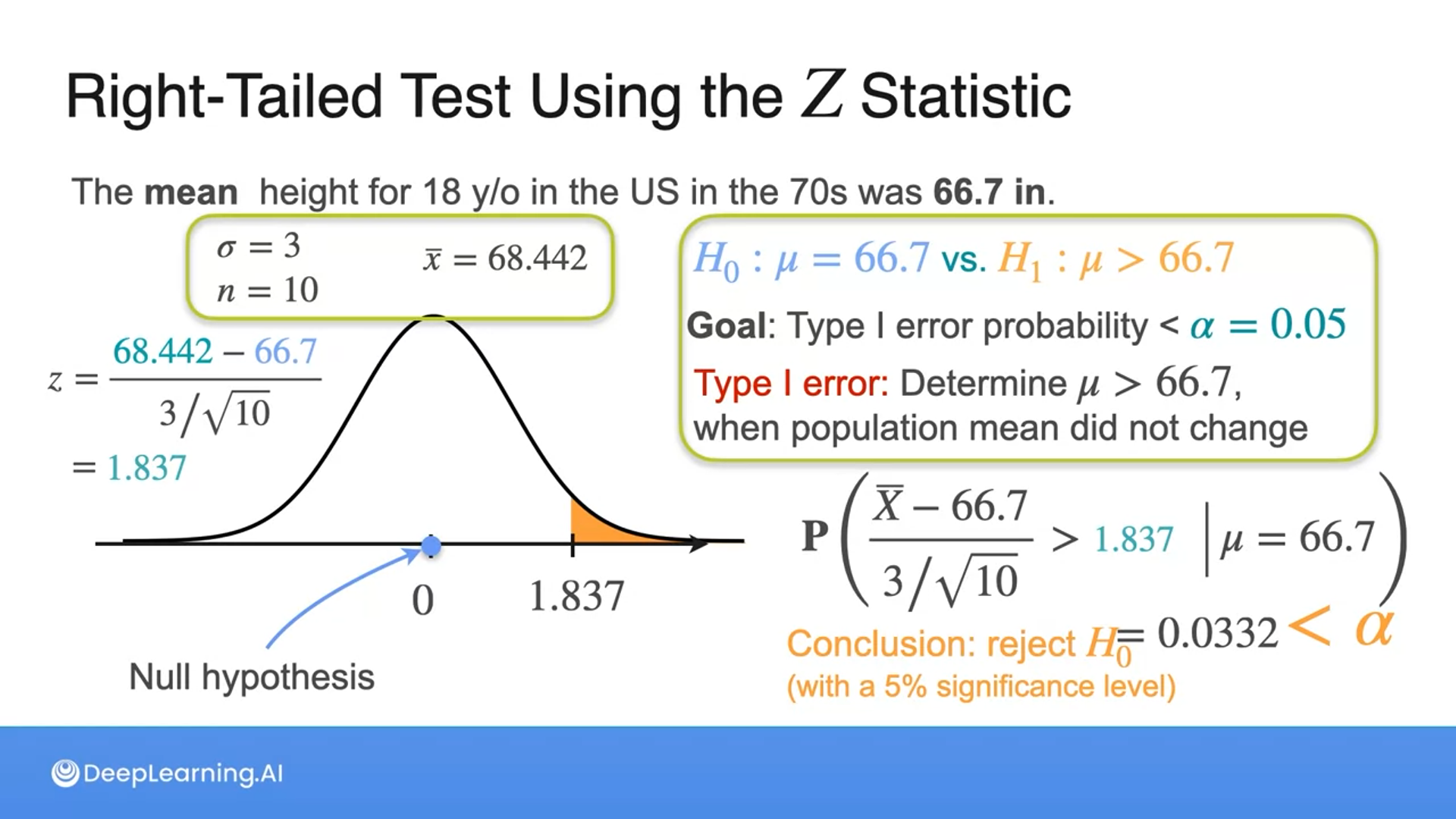
If the null hypothesis $H_0$ states that the mean height for 18-year-olds in the US in the 1970s was 66.7 inches or $𝐻_0:𝜇=66.7$, and the alternative hypothesis $H_1$ is that the mean height is less than 66.7 inches or $𝐻_0:𝜇<66.7$, which statement correctly identifies a type 1 error and a type II error in this context?
- Type I error: Determining that $𝜇<66.7$ when the population mean did not change. Type II error: Determining that $μ=66.7$ when $μ<66.7$ is true.
- Type I error: Determining that $μ<66.7$ when $𝜇≥66.7$ is true. Type II error: Determining that $μ=66.7$ when $𝜇≥66.7$ is true.
- Type I error: Determining that $μ=66.7$ when $𝜇<66.7$ is true. Type II error: Determining that $𝜇<66.7$ when the population mean did not change.
Answer
1
Great job! A type I error occurs when we incorrectly reject the null hypothesis when it is true, while a type II error occurs when we fail to reject the null hypothesis when it is false.
p-Value


The p-value measures how well the sample is moderate under the null hypothesis.
A small p-value says that the sample landed on the tail of the distribution under $H_0$, so they’re pretty unlikely to happen if $H_0$ was true.




Which of the following statements about the p-value is true?
- If the p-value is less than $α$ (significance level), then you reject the null hypothesis.
- The p-value represents the probability of observing the data or more extreme results under the assumption that the null hypothesis is true.
- A smaller p-value indicates stronger evidence against the null hypothesis.
Answer
1
Great job! You reject the null hypothesis if the p-value is less than alpha (significance level). This decision rule is commonly used in hypothesis testing to determine whether the observed data provides enough evidence to reject the null hypothesis.
2
Yes! The p-value represents the probability of observing the data or more extreme results under the assumption that the null hypothesis is true. It helps assess the strength of evidence against the null hypothesis based on the observed data.
3
Great job! A smaller p-value indicates stronger evidence against the null hypothesis. When the p-value is small, it suggests that the observed data are unlikely to have occurred if the null hypothesis were true, leading to the rejection of the null hypothesis.



TL; DR;
A p-value is the probability of the observed data occurring if the null hypothesis is true.
Since we do observe the data (sample) if the p-value is lower than the significance level ($\alpha$), then we reject the null hypothesis because it’s like saying the sample we observe is taken as the extreme value by the null hypothesis point of view, when it’s not.
A value for $\alpha$ is usually 0.05 and in some tight cases it’s 0.01.
Critical Values
A critical value is a value (extreme sample) at the p-value ($\alpha)$ so we can still reject $H_0$.
A critical value is usually referred to as $k_{\alpha}$.

One good thing about critical values is that we can make a decision based on the observed statistics without needing to calculate the p-value.
If the significance level (alpha) in a hypothesis test is changed from 0.05 to 0.01, what will happen to the critical value or k-value?
The critical value or k-value increases
Changing the significance level (alpha) from 0.05 to 0.01 increases the critical value or k-value. This means that the threshold for which we reject the null hypothesis increases.




Power of a Test


Type 1 error is the significance level, so it happens for one value of the population mean.
The significance level is the maximum probability of making a type 1 error, which should always be small.
Type 2 error can happen for any population mean values that are bigger than the population mean of the null hypothesis.
In our example, a type 1 error cares about the value 66.7 in, but a type 2 error can happen for any population mean bigger than 66.7 in.
So we need a probability to calculate a type 2 error.
The sample mean follows the Gaussian distribution but shifted since we have a sample mean of 70 instead of 66.7, so the probability of not rejecting $H_0$ is the blue area on the left of the Gaussian distribution.
This probability of type 2 error is called beta.
The probability doesn’t depend on the observed sample, but only on the significance level that we chose for the test.


The power of the test is a function that tells us the probability of rejecting the null hypothesis for each possible value of the population, meaning the alternative hypothesis.
The power of a test is the probability of rejecting the null hypothesis given that the population mean is in the alternative hypothesis and it’s 1 minus the type 2 error probability.



The population mean determines the mean of the distribution of the sample mean and the distribution follows the normal distribution.
As the population mean increases, the probability that the sample mean is smaller than the critical value decreases (the probability of the null hypothesis is false and it’s false) because the critical value gets further away from the normal distribution.
Interpreting Results




The p-values are the criterion for making a decision based on the data and are not the probability of $H_0$ being true.
A p-value is the probability of seeing the observed data in the Gaussian distribution of the null hypothesis and when it’s small, the chance is also small.
A reminder that we don’t accept the null hypothesis when we don’t reject the null hypothesis.
All the information provided is based on the Probability & Statistics for Machine Learning & Data Science | Coursera from DeepLearning.AI





 }
}