▤ 목차
Neural Networks Basics
Quiz
Q1
In logistic regression, given $\bf x$ and parameters $w ∈ {\mathbb R^{n_x}}, b∈{\mathbb R}$. Which of the following best expresses what we want $\hat y$ to tell us?
Choice
- $\sigma(W \textbf{x} + b)$
- $P(y = \hat y | x)$
- $\sigma(W \bf x)$
- $P(y = 1|\bf x)$
Hint
Remember that we are interested in the probability that $y=1$.
Answer
4
Yes. We want the output $\hat y$ to tell us the probability that $y=1$ given $x$.
Q2
Which of these is the “Logistic Loss”?
Choice
- $\mathcal{L^{(i)}}(\hat{y^{(i)}}, y^{(i)})=max(0, y^{(i)}-\hat y^{(i)})$
- $\mathcal{L^{(i)}}(\hat{y^{(i)}}, y^{(i)})=|y^{(i)}-\hat y^{(i)}|$
- $\mathcal{L^{(i)}}(\hat{y^{(i)}}, y^{(i)})=|y^{(i)}-\hat y^{(i)}|^2$
- $\mathcal{L^{(i)}}(\hat{y}^{(i)}, y^{(i)})=-(y^{(i)} \log \hat y^{(i)}+(1-y^{(i)}) \log (1-\hat y^{(i)}))$
Answer
4
Correct, this is the logistic loss you've seen in the lecture!
Q3
Suppose that $\hat y = 0.9$ and $y=1$. What is the value of the "Logistic Loss"? Choose the best option.
Choice
- 0.105
- $\mathcal{L}(\hat{y}, y)=-(\hat{y} \log y+(1-\hat{y}) \log (1-y))$
- $+\infty$
- 0.005
Answer
1
Yes. Since $\mathcal{L}(\hat{y}, y)=-(y \log \hat y+(1-y) \log (1-\hat y))$, for the given values we get $\mathcal{L}(0.9, 1)=-(1 \log 0.9 +(1-1) \log (1-0.9))$
Q4
Suppose x is a (8, 1) array. Which of the following is a valid reshape?
Choice
- x.reshape(2, 2, 2)
- x.reshape(1, 4, 3)
- x.reshape(2, 4, 4)
- x.reshape(-1, 3)
Answer
1
Yes. This generates uses 222 = 8 entries.
Q5
Suppose img is a (32, 32, 3) array, representing a 32x32 image with 3 color channels red, green and blue. How do you reshape this into a column vector $x$?
Choice
- $x$ = img.reshape((1, 32*32, 3))
- $x$ = img.reshape((32323, 1))
- $x$ = img.reshape((3, 32*32))
- $x$ = img.reshape((32*32, 3))
Answer
2
Q6
Consider the following random arrays $a$, $b$, and $c$:

What will be the shape of $c$?
Choice
- The computation cannot happen because it is not possible to broadcast more than one dimension
- c.shape = (2, 3, 3)
- c.shape = (3,3)
- c.shape = (2, 1)
Answer
1
Yes. It is not possible to broadcast together a and b. In this case there is no way to generate copies of one of the arrays to match the size of the other.
Q7
Consider the two following random arrays $a$ and $b$:

What will be the shape of $c$?
Choice
- The computation cannot happen because the sizes don't match. It's going to be "Error"!
- c.shape = (4, 3)
- c.shape = (3, 3)
- c.shape = (4,2)
Answer
1
Indeed! In numpy the "*" operator indicates element-wise multiplication. It is different from "np.dot()". If you would try "c = np.dot(a,b)" you would get c.shape = (4, 2).
Q8
Suppose you have $n_x$ input features per example. If we decide to use row vectors $\textbf{x}_j$ for the features and $X=\left[\begin{array}{c} \mathbf{x}_1 \\ \mathbf{x}_2 \\ \vdots \\ \mathbf{x}_m \end{array}\right]$
What is the dimension of $X$?
Choice
- $(n_x,n_x)$
- $(n_x,m)$
- $(m,n_x)$
- $(1,n_x)$
Answer
3
Yes. Each $\textbf{x}_j$ has dimension $1 \times n_x$, $X$ is built stacking all rows together into a $m \times n_x$ array.
Q9
Suppose you have $n_x$ input features per example. Recall that $X = [x^{(1)}x^{(2)} \dots x^{(m)}]$. What is the dimension of X?
Choice
- $(m,1)$
- $(n_x,m)$
- $(1,m)$
- $(m,n_x)$
Answer
2
Yes. Each $x$ has dimension $n_x \times 1$, $X$ is built stacking all columns together into a $n_x \times m$ array
Q10
Consider the following array:
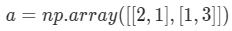
What is the result of $np.dot(a,a)$?
Choice
- The computation cannot happen because the sizes don't match. It's going to be an "Error"!
- ${4\,1 \choose 1\,9}$
- ${5\,5 \choose 5\,10}$
- ${4\,2 \choose 2\,6}$
Answer
3
Yes, recall that * indicates the element-wise multiplication and that np.dot() is the matrix multiplication.
Q11
Suppose our input batch consists of 8 grayscale images, each of dimension 8x8. We reshape these images into feature column vectors $\textbf x^j$. Remember that $X=[\textbf x^{(1)}\textbf x^{(2)} ⋯\textbf x^{(8)}]$. What is the dimension of $X$?
Choice
- (64, 8)
- (8, 64)
- (8, 8, 8)
- (512, 1)
Hint
After converting the 8x8 grayscale images to a column vector we get a vector of size $64$, thus $X$ has dimension $(64,8)$.
Answer
1
Q12
Recall that $np.dot(a, b)$performs a matrix multiplication on $a$ and $b$, whereas $a ∗ b$ performs an element-wise multiplication. Consider the two following random arrays $a$ and $b$:

What will be the shape of $c$?
Choice
- c.shape = (12288, 150)
- c.shape = (150,150)
- c.shape = (12288, 45)
- The computation cannot happen because the sizes don't match. It's going to be "Error"!
Answer
3
Correct, remember that a np.dot(a, b) has shape (number of rows of a, number of columns of b). The sizes match because: "number of columns of a = 150 = number of rows of b”
Q13
Consider the following code snippet:
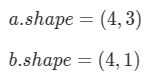
for i in range(3):
for j in range(4):
c[i][j] = a[j][i] + b[j]How do you vectorize this?
Choice
- c = a.T + b
- c = a + b
- c = a.T + b.T
- c = a + b.T
Hint
Notice that b is a column vector; but we are using it to fill the row i of c.
Answer
3
Yes. a[j][i] being used for a[i][j] indicates we are using a.T, and the element in the row j is used in the column j thus we are using b.T.
Q14
Consider the following code:

What will be $c$? (If you’re not sure, feel free to run this in python to find out).
Choice
- This will invoke broadcasting, so b is copied three times to become (3, 3), and ∗∗ invokes a matrix multiplication operation of two 3x3 matrices so c.shape will be (3, 3)
- It will lead to an error since you cannot use “*” to operate on these two matrices. You need to instead use np.dot(a,b)
- This will multiply a 3x3 matrix a with a 3x1 vector, thus resulting in a 3x1 vector. That is, c.shape = (3,1).
- This will invoke broadcasting, so b is copied three times to become (3,3), and ∗∗ is an element-wise product so c.shape will be (3, 3)
Answer
4
Q15
Consider the following computational graph.
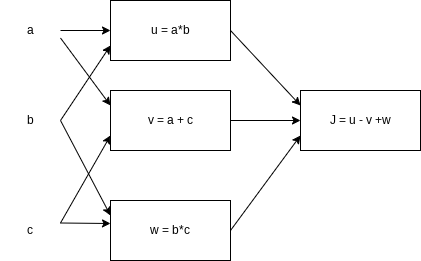
What is the output of J?
Choice
- $(a-1), (b+c)$
- $(a + c), (b-1)$
- $(c-1), (a + c)$
- $ab + bc + ac$
Answer
2
Yes. $J=u-v+w=a b-(a+c)+b c=a b-a+b c-c=a(b-1)+c(b-1)=(a+c) (b-1)$
All the information provided is based on the Deep Learning Specialization | Coursera from DeepLearning.AI
'Coursera > Deep Learning Specialization' 카테고리의 다른 글
| Neural Networks and Deep Learning (7) (1) | 2024.11.25 |
|---|---|
| Neural Networks and Deep Learning (6) (0) | 2024.11.23 |
| Neural Networks and Deep Learning (4) (0) | 2024.11.17 |
| Neural Networks and Deep Learning (3) (0) | 2024.11.14 |
| Neural Networks and Deep Learning (2) (0) | 2024.11.13 |






 }
}