▤ 목차
Shallow Neural Networks
Shallow Neural Network
Activation Functions

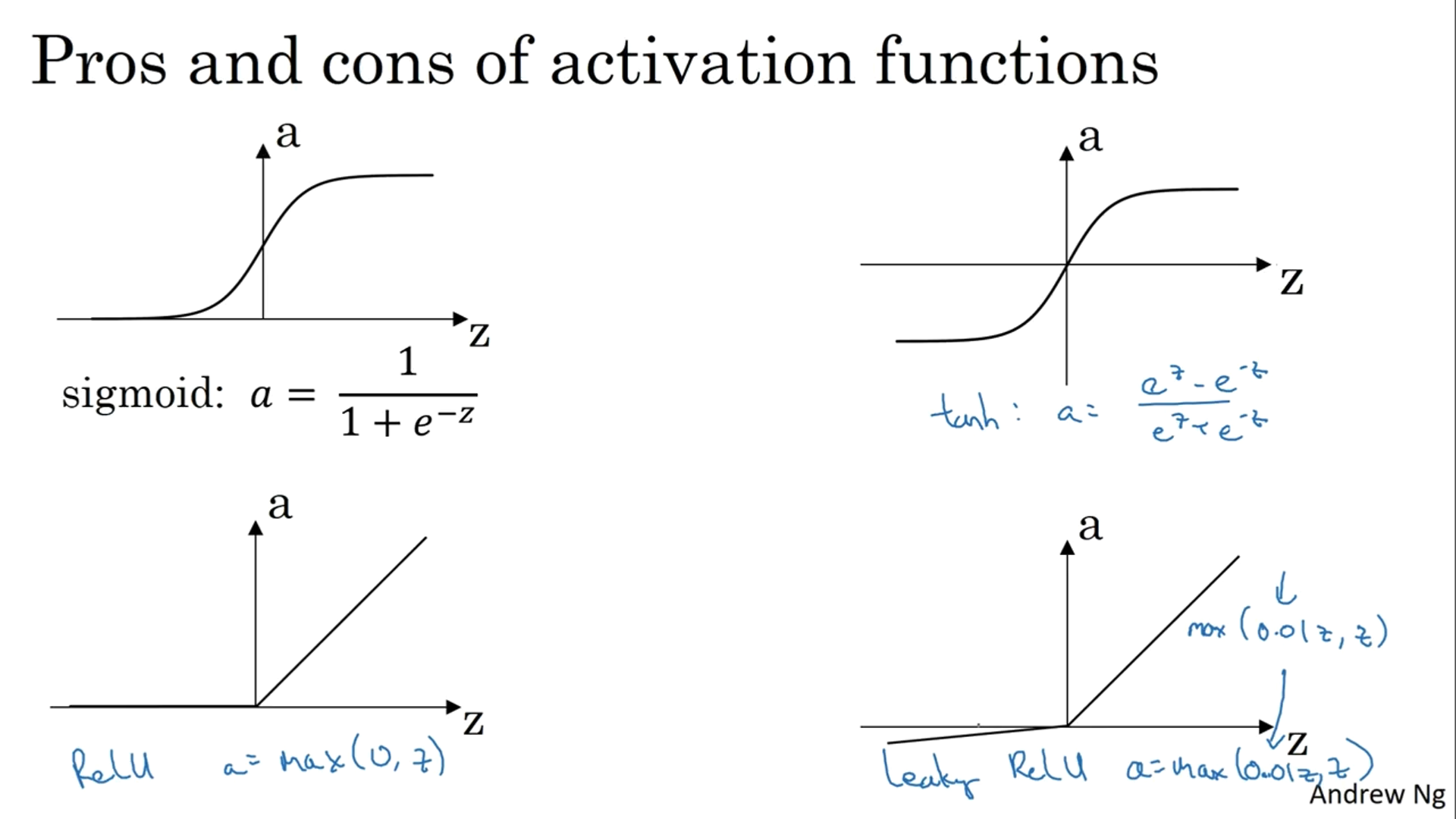
So far we’ve been using sigmoid as our activation function, but we can use other activation functions such as hyperbolic tangent, aka tanh.
Tanh falls within the interval between -1 and 1 and, when plotted, looks like a shifted sigmoid function.
Using tanh can center your data to have a mean of 0 rather than 0.5 when using a sigmoid function to ease the learning for the next layer.
We generally don’t use a sigmoid as an activation function except in the output layer when we need to output a probability to classify 2 classes.
One downside of both sigmoid and tanh is when z is either very large or small, then the gradient of this function becomes very small and can slow down the gradient descent.
One commonly used activation function nowadays is a rectified linear unit (ReLU) where it zeroes out if the values are negative and if the values are positive, then the gradients stay at 1.
Why do you need Non-Linear Activation Functions?

When we don’t use a non-linear activation function, we call it a linear activation function or an identity activation function.
The reason we use a non-linear activation function is to add some dynamics (changes) to the network so it can learn and tweak parameters to get close to the answer.
Using a linear activation function outputs a linear function (wx + b) constantly and passes the previous information without any changes.
So there’s no point in stacking many layers if we aren’t using a non-linear function.
We generally don’t use a linear activation function except in the output layer when we need to output a real number instead of a probability for a regression problem (e.g. predicting house prices).
Derivatives of Activation Functions
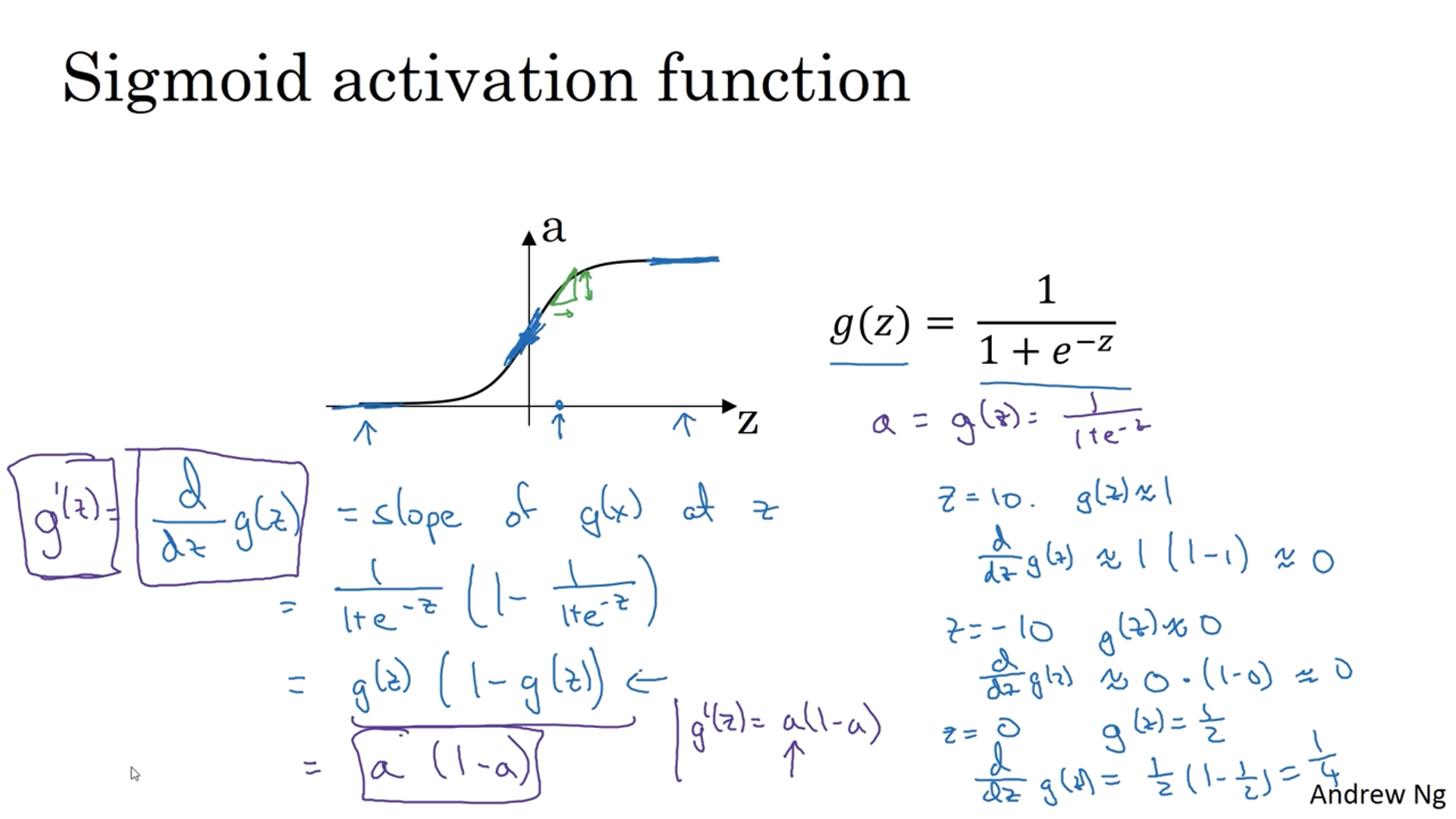
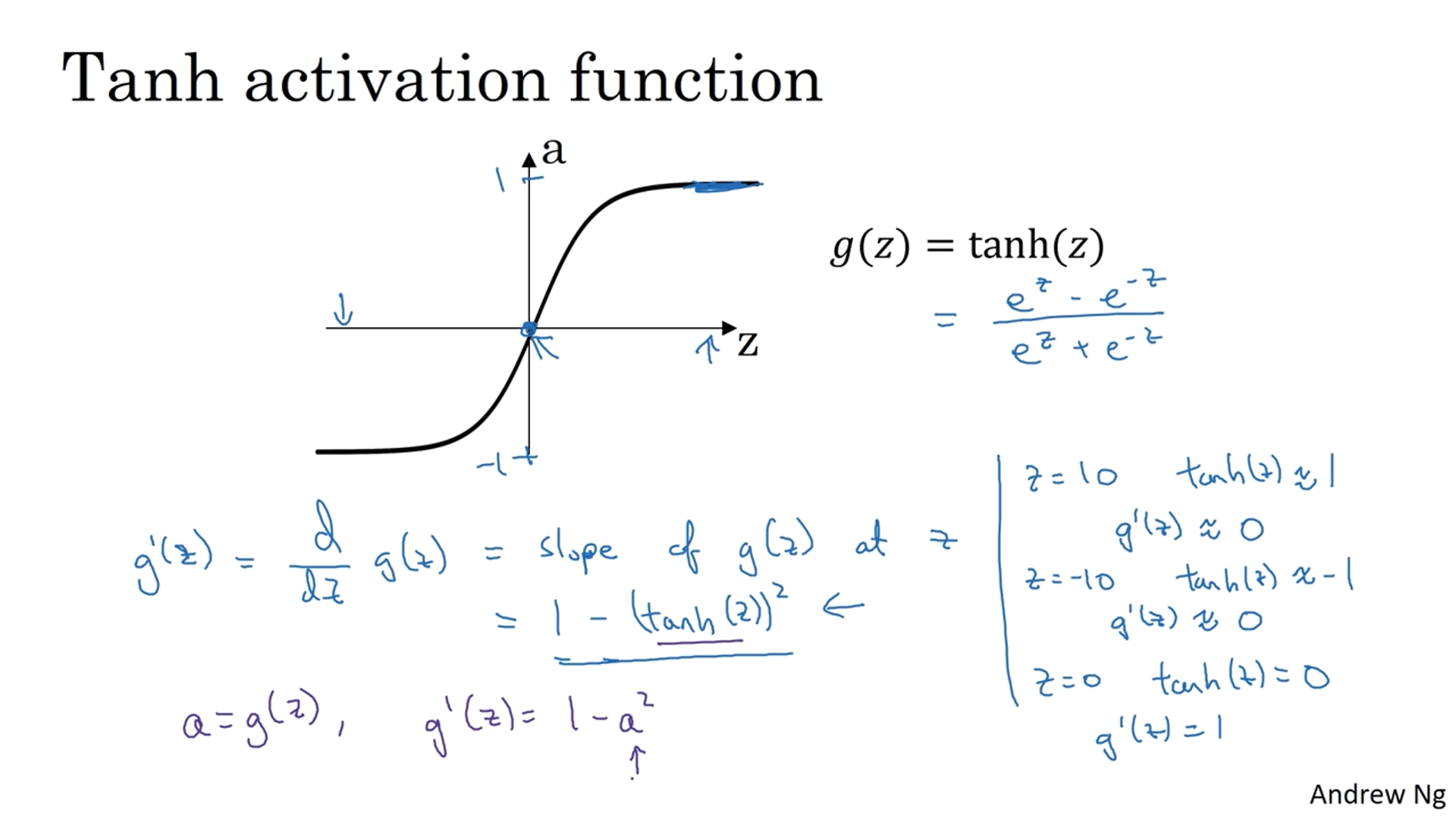

In our examples, $a$ equals to $g'(z)$ (the derivative of $g(x)$ at $z$).
The derivative of a sigmoid activation function is $a * (1-a)$ and when $z$ is very large or small the gradient gets close to $0$ and when it’s $0.5$ or $1/2$, then the gradient is $0.25$ or $1/4$.
The derivative of a tanh function is $1-a^2$ and when $z$ is very large or small the gradient gets close to $0$ and when it’s $0$, then the gradient is $1$.
The derivative of ReLU is $0$ when $z <0$ and $1$ when $z >0$ or $z\ge0$ since the chance of z being $0$ is very unlikely.
The derivative of Leaky ReLU is $0.01$ when $z<0$ and $1$ when $z>0$ or $z\ge 0$.
Gradient Descent for Neural Networks


Gradient descent computes the partial derivatives for each variable and then updates the value to get closer to the answer.
Backpropagation Intuition

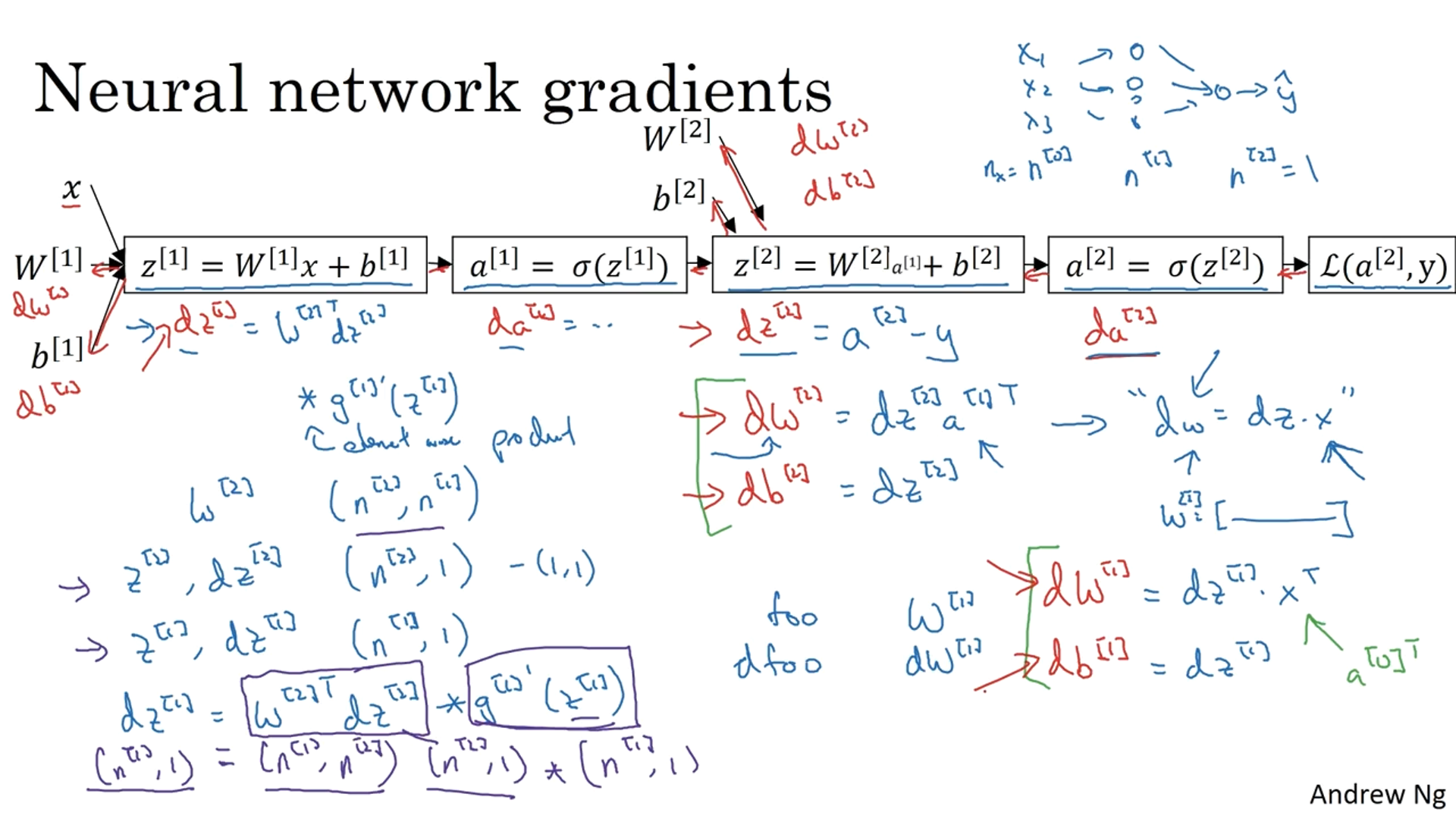


The variable and its derivative have the same dimensions.
One tip in backpropagation is to match the shapes correctly to eliminate the bugs/errors.
Random Initialization


Apart from logistic regression, it’s important to initialize the weights randomly.
When we initialize our weights to 0, then the nodes in the layer become identical, meaning the nodes (hidden units) are computing the same function and have the same influence on the output unit.
This leads to having no purpose other than having a single node in the layer because what we want is for hidden units to compute different functions rather being being the same.
The reason we multiply random values by 0.01 (or any small numbers) is to initialize with small numbers to avoid slowing down the learning process.
If activation functions like sigmoid or tanh are used and the values are high, then the gradients get close to 0 and slow down the learning.
All the information provided is based on the Deep Learning Specialization | Coursera from DeepLearning.AI
'Coursera > Deep Learning Specialization' 카테고리의 다른 글
| Neural Networks and Deep Learning (9) (1) | 2024.11.27 |
|---|---|
| Neural Networks and Deep Learning (8) (1) | 2024.11.26 |
| Neural Networks and Deep Learning (6) (1) | 2024.11.23 |
| Neural Networks and Deep Learning (5) (2) | 2024.11.18 |
| Neural Networks and Deep Learning (4) (1) | 2024.11.17 |





 }
}