Optimization in Neural Networks and Newton’s Method
Quiz
Q1
Given the single-layer perceptron described in the lectures:

What should be replaced in the question mark?
- $w_1w_2+x_1x_2+b$
- $w_1x_1+w_2x_2+b_1+b_2$
- $w_1x_1+w_2x_2+b$
- $w_1x_2+w_2x_1+b$
Answer
3
Correct! In a single-layer perceptron, we evaluate a (weighted) linear combination of the inputs plus a constant term, representing the bias!
Q2
For a Regression using a single-layer perceptron, select all that apply:
- The loss function used is $L(y,\hat y) = -y\ln(\hat y)-(1-y)\ln(1-\hat y)$
- The loss function used is $L(y,\hat y) = {1\over 2}(y-\hat y)^2$
- To minimize the loss function, we consider $L(y, \hat y)$ as a function of $w_1, w_2,$ and $b$
- To minimize the loss function, we consider $L(y, \hat y)$ as a function of $x_1$ and $x_2$
Answer
2
Correct! This is the mean squared error, usually used as a loss function for regression.
3
Correct! We see the Loss Function as a function of $w_1,w_2,$ and $b$ so we can perform Gradient Descent to find the optimal parameters that minimize it!
Q3
Consider the problem of Classification using a single-layer perceptron as discussed in the lectures.
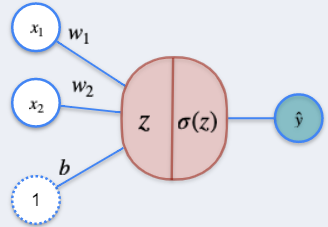
In the figure above, $z$ and $σ(z)$ are, respectively:
- $z = w_1x_1+w_2x_2+b$ and $\sigma(z)={1\over2}(z-\hat z)^2$
- $z = {1\over 1+e^{-z}}$ and $\sigma(z) = w_1x_1+w_2x_2+b$
- $z = x_1+x_2+b$ and $\sigma(z)={1\over2}(z-\hat z)^2$
- $z = w_1x_1+w_2x_2+b$ and $\sigma(z) = {1\over 1+e^{-z}}$
Answer
4
Correct! In this case, z is a linear combination of the inputs, and $σ(z)$ is the sigmoid function, so it maps the result to a value between 0 and 1, thus the output can be interpreted as a probability.
Q4
In the 2,2,1 Neural Network described below
How many parameters must be tuned to minimize the Loss Function?
- 2
- 3
- 6
- 9
Answer
4
Correct! We have 2 inputs, which will generate 2 constant terms ($b_1$ and $b_2$). Since the next layer has 2 neurons, each input must have 2 parameters. Therefore, the first layer has 2 + 2*2 = 6 parameters. The hidden layer, therefore, has three more parameters since there are 2 neurons. We also must add another constant term, $c$. In total, there are 9 parameters.
Q5
About Backpropagation, check all that apply:
- It is a way to obtain the input values for a given output of a neural network.
- It is a method to update the parameters of a neural network.
- It is the same as gradient descent.
- It is a method that starts in the output layer and finishes in the input layer.
Hint
Even though the main idea behind backpropagation uses gradient descent to update the neural network parameters, it is not gradient descent itself.
Answer
2
Correct! This is the method by which a neural network updates its parameters.
4
Correct! As the name suggests, the backpropagation method iteratively updates the neural network parameters from backward.
All the information provided is based on the Calculus for Machine Learning and Data Science | Coursera from DeepLearning.AI
'Coursera > Mathematics for ML and Data Science' 카테고리의 다른 글
| Probability & Statistics for Machine Learning & Data Science (0) (0) | 2024.09.02 |
|---|---|
| Calculus for Machine Learning and Data Science (11) (3) | 2024.09.01 |
| Calculus for Machine Learning and Data Science (9) (3) | 2024.08.30 |
| Calculus for Machine Learning and Data Science (8) (2) | 2024.08.29 |
| Calculus for Machine Learning and Data Science (7) (2) | 2024.08.28 |





 }
}