Gradients and Gradient Descent
Gradient Descent
Optimization using Gradient Descent in one variable - Part 1

It’s hard to find the lowest point using the formula above.

So we can try something different by trying points in both directions and then choosing a point that’s lower than the other 2.
But this also takes a long time.
The lecturer introduces a term, called the "learning rate", denoted by $a$ in the equation.
$$ 0.05 \mapsto 0.05+a \cdot \frac{d}{d x} f(0.05) $$
In this case, what is the purpose of the learning rate?
Ensure that the "steps" are small enough.
Correct! The learning rate ensures that the steps we are performing are small enough so the algorithm can converge to the minimum.
Optimization using Gradient Descent in one variable - Part 2

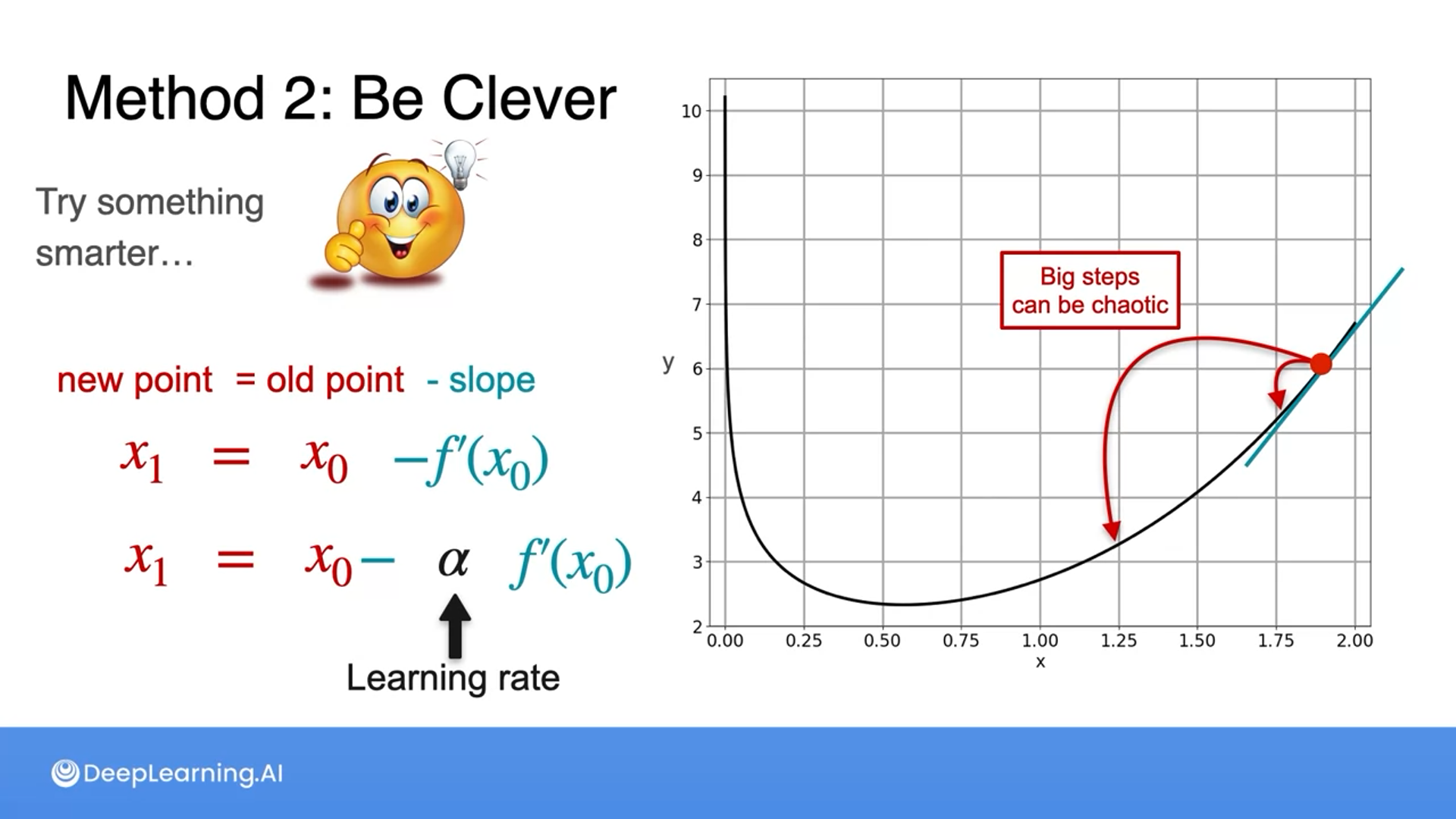



Depending on the sign of the slope, we can take the steps either to the left or right.
The caveat is if the slope is steep, then steps can be large and chaotic, hence we multiply a small number by the slope, which is called a learning rate.
By applying a learning rate, if the slope is big, it can take a large step and if the slope is small, it can take a smaller step.
We are not solving for the slope to find the $x$, instead, we input the previous output as $x$ along with the learning rate to get the new $x$.
Optimization using Gradient Descent in one variable - Part 3


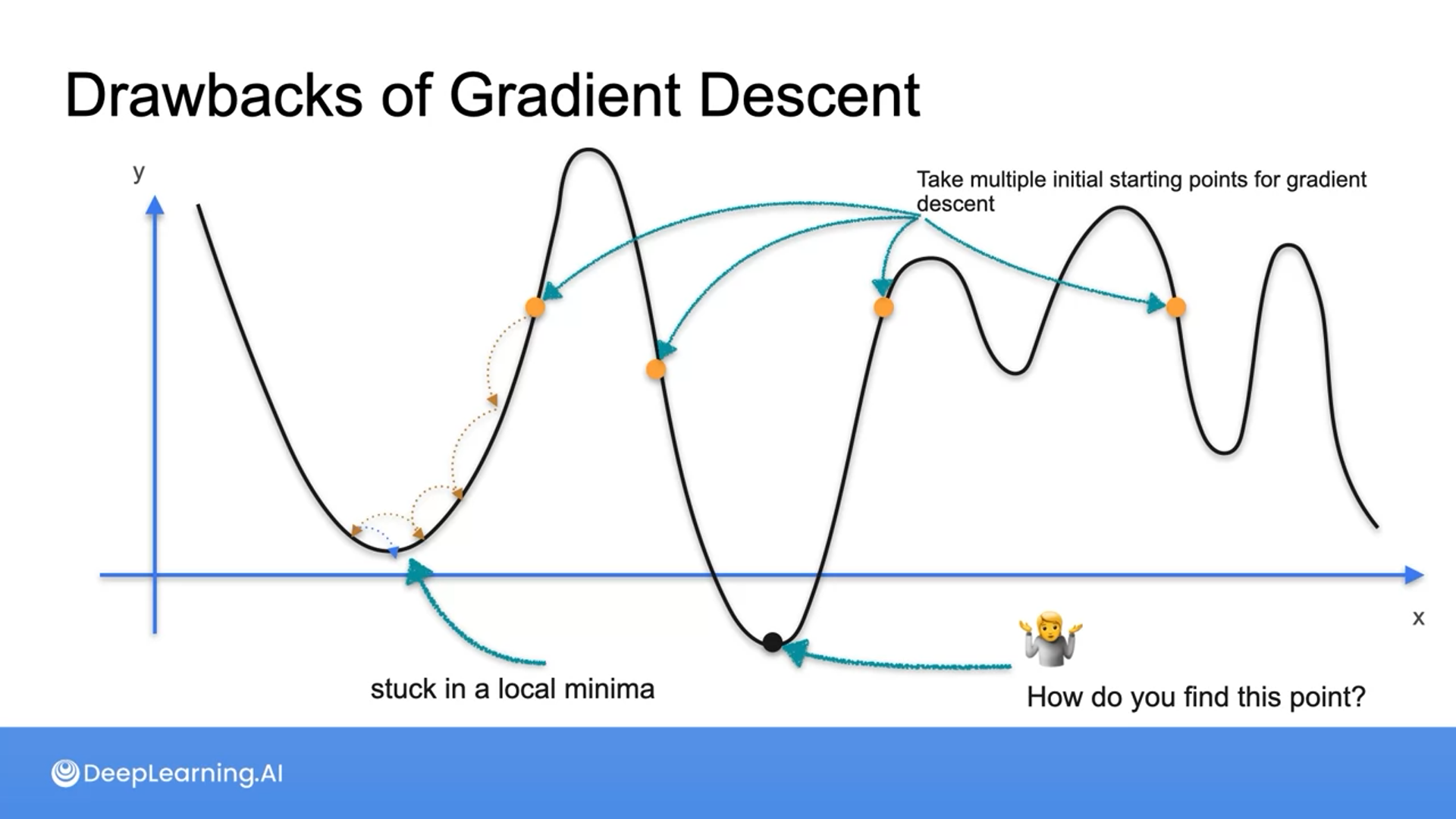
There’s no set best learning rate and this is something we always have to experiment.
The drawback of the gradient descent is that it moves based on the slope and won’t always find the global minima.
Optimization using Gradient Descent in two variables - Part 1

We use gradients to find the coldest place.
Optimization using Gradient Descent in two variables - Part 2
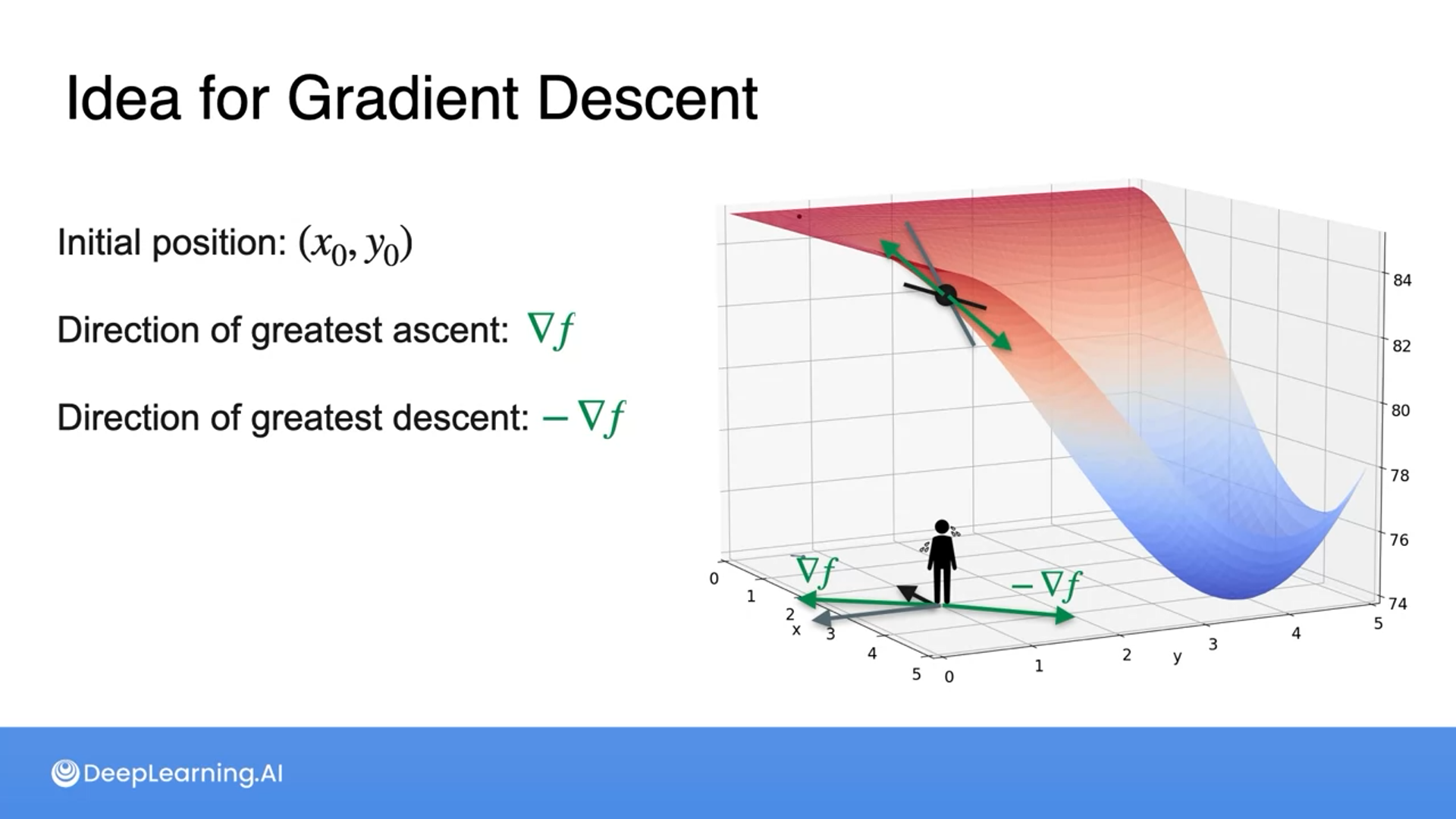

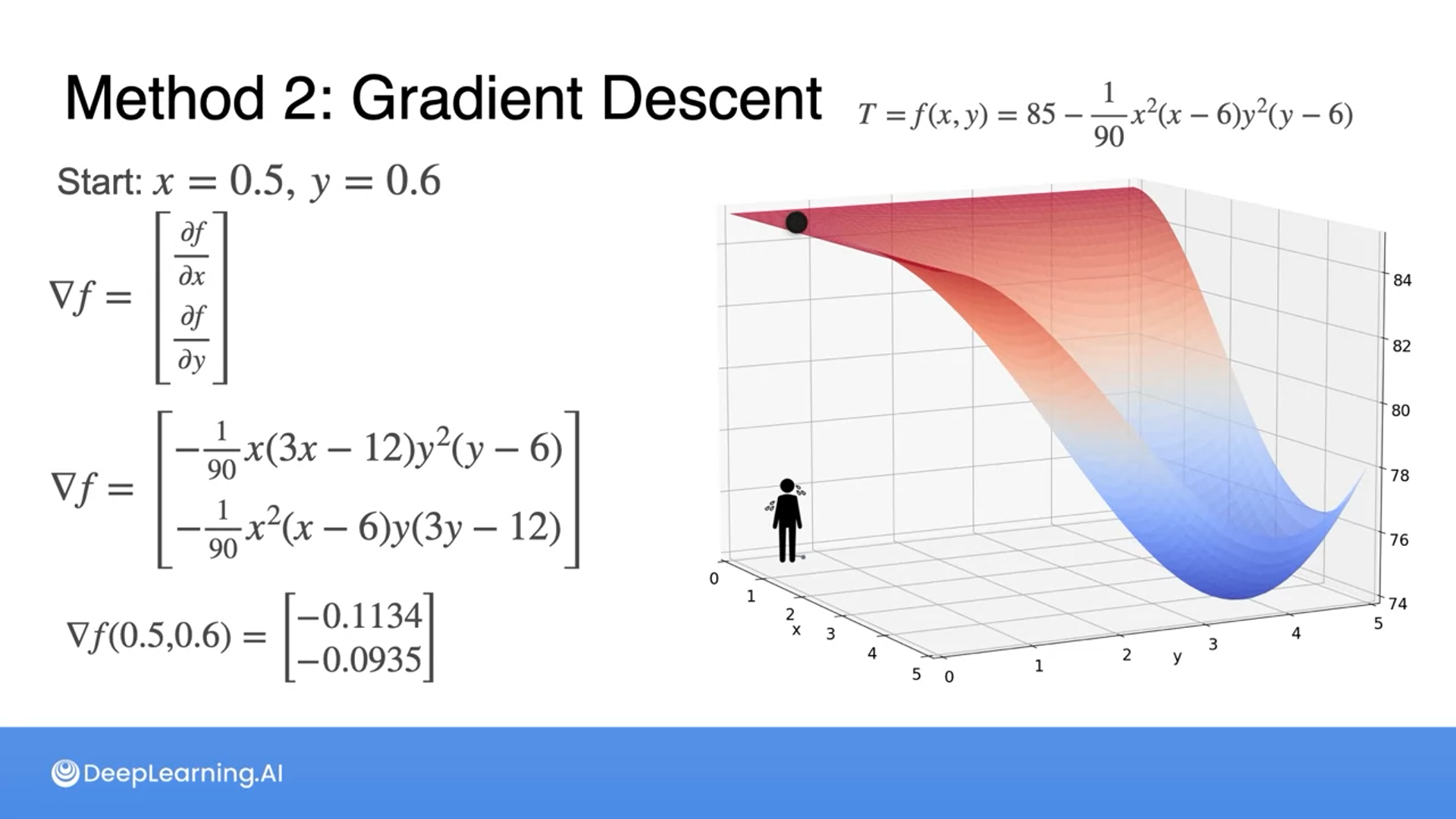
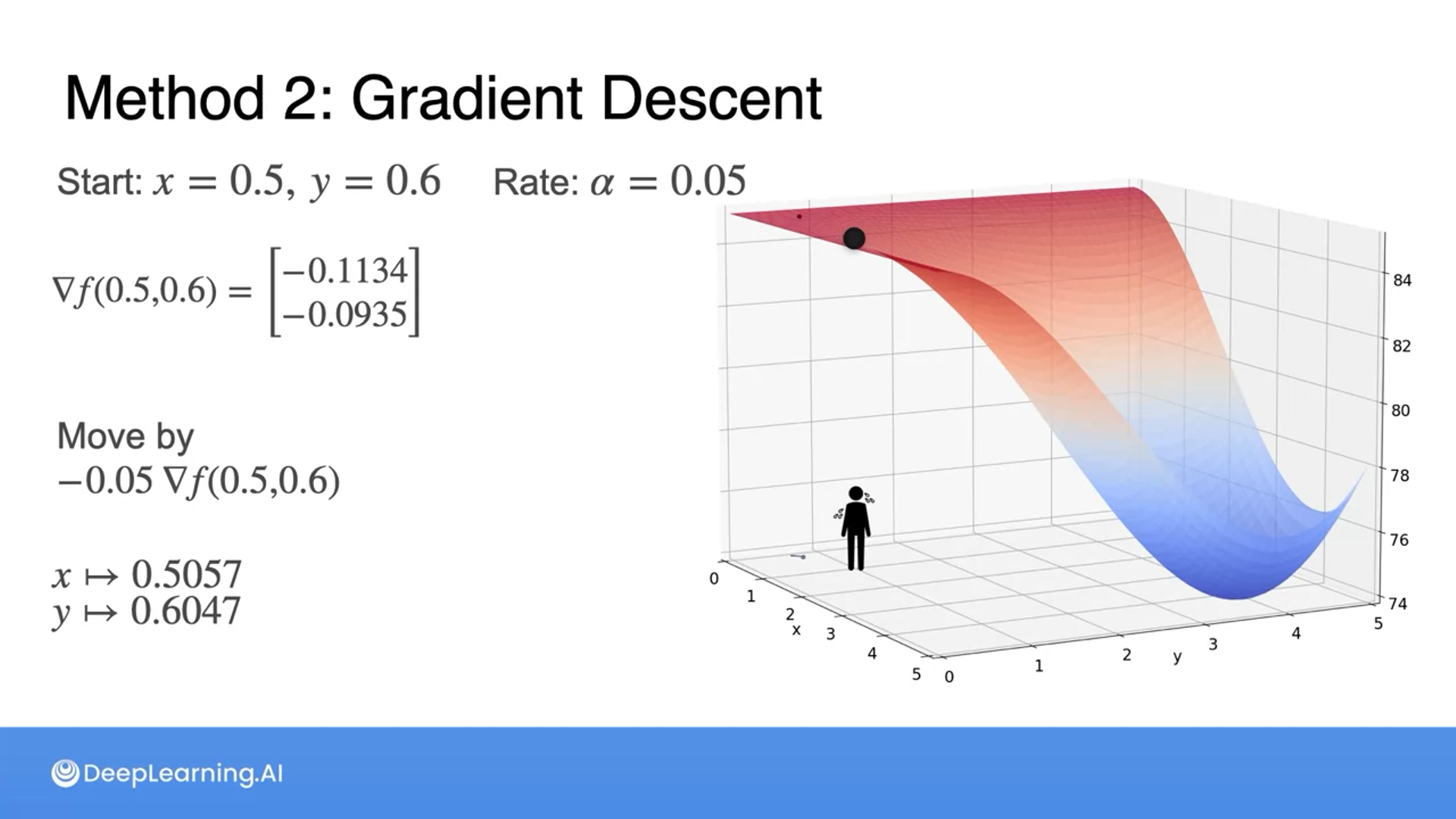



We get the gradients of variables and get a vector direction by adding the gradients.
Then multiply by the learning rate to get to a new point.
Optimization using Gradient Descent - Least squares

Optimization using Gradient Descent - Least squares with multiple observations



At an initial point, we update the variables m and b to minimize the loss.
All the information provided is based on the Calculus for Machine Learning and Data Science | Coursera from DeepLearning.AI
'Coursera > Mathematics for ML and Data Science' 카테고리의 다른 글
| Calculus for Machine Learning and Data Science (10) (3) | 2024.08.31 |
|---|---|
| Calculus for Machine Learning and Data Science (9) (3) | 2024.08.30 |
| Calculus for Machine Learning and Data Science (7) (2) | 2024.08.28 |
| Calculus for Machine Learning and Data Science (6) (1) | 2024.08.27 |
| Calculus for Machine Learning and Data Science (5) (0) | 2024.08.26 |





 }
}