Probability & Statistics for Machine Learning & Data Science (14)

Describing probability distributions and probability distributions with multiple variables

Quiz

728x90

Q1

Consider the four sets of samples above. Which one has the smallest variance?

$$ \begin{array}{c|cccc}\hline \text { Set } & \text { Values } & & & \\ \hline 1 & 1 & 5 & 7 & 9 \\2 & -20 & -10 & 0 & 10 \\3 & 100 & 101 & 102 & 103 \\4 & -10 & -5 & 0 & -5 \\\hline\end{array} $$

1. 1
2. 2
3. 3
4. 4

Answer

3

The variance measures how much a sample is spread. We can easily look at all the samples and check that this one has the smallest spread.

Q2

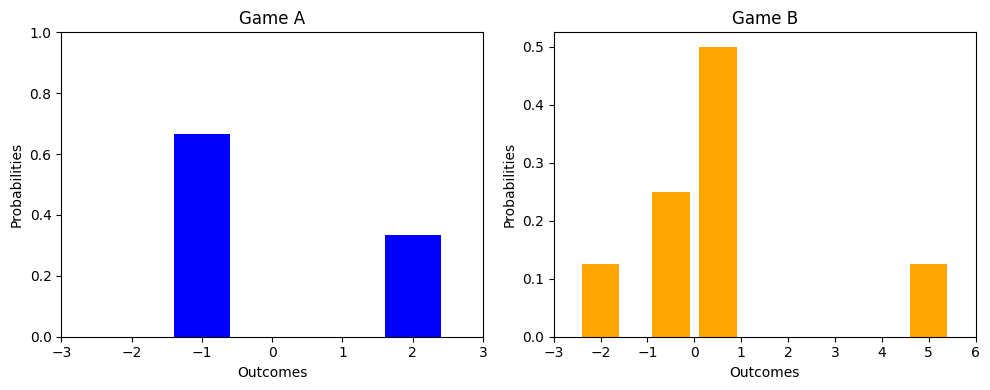
Consider two games, Game A and Game B, each with different probability distributions of winnings and losses. Game A has a probability of 1/3 to win $2 and a probability of 2/3 to lose $1. Game B has a probability of 1/2 to win $0.50, a probability of 1/4 to lose $0.50, a probability of 1/8 to win $5, and a probability of 1/8 to lose $2.

Which of the following statements is true?

1. Both Game A and Game B have the same kurtosis.
2. Game A's kurtosis is smaller than Game B's kurtosis.
3. Game B's kurtosis is smaller than Game A's kurtosis.

Answer

2

Kurtosis measures the shape and thickness of the rails of a probability distribution. A larger kurtosis indicates thicker tails and more extreme values. In this case, Game Y has a larger kurtosis because it has thicker tails due to the presence of extreme values (winning $5 or losing $2 with small probabilities).

Consider the following independent random variables:

$$ X \sim \text{Normal}(3,1)\\ Y \sim \text{Normal}(2,2) $$

Then $Z=X+Y \sim \text{Normal}(\mu,\sigma)$, where $\mu, \sigma$ are equal to:

1. $\mu=\sqrt5, \sigma=\sqrt3$
2. $\mu=5, \sigma=\sqrt5$
3. $\mu=5, \sigma=\sqrt3$
4. $\mu=5, \sigma=5$

Hint

Remember the formula for a sum of independent Gaussians, $\mu Z = \mu X + \mu Y$, and $\sigma Z = \sqrt{\sigma^2X + \sigma^2Y}$

Answer

2

Q4

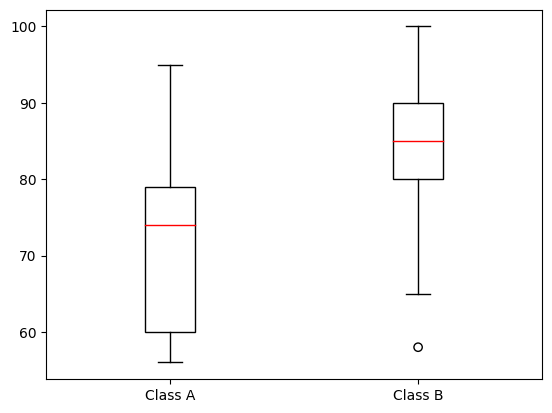
Consider the following box plot for the test scores of two classes, A and B:

Which of the following statements is true?

1. Class B's interquartile range (IQR) is larger than Class A's interquartile range.
2. Class B's median score is higher than Class A's median score.
3. Class A's interquartile range (IQR) is larger than Class B's interquartile range.
4. Class A's median score is higher than Class B's median score.

Answer

2

Looking at the box plot, we can see that the median of Class A is around 75, while the median of Class B is around 85.

3

The rectangle in A is bigger than B.

Q5

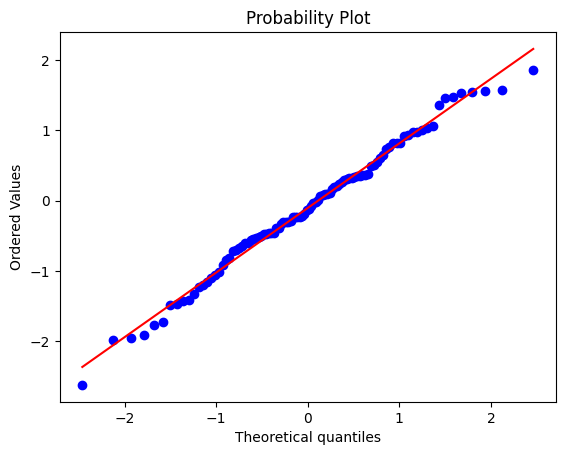
Consider the following QQ plot for a set of data:

Which of the following statements is true?

1. The data has a lower variance than a normal distribution.
2. The data is not normally distributed.
3. The data looks normally distributed.
4. The data has a higher variance than a normal distribution.

Hint

The variance of the data cannot be determined from the QQ plot.

Answer

3

The QQ plot compares the observed data with the theoretical quantiles of a normal distribution. If the points lie close to the diagonal line, then the data is likely normally distributed.

All the information provided is based on the Probability & Statistics for Machine Learning & Data Science | Coursera from DeepLearning.AI